The Logic Café
Reference
Chapter Seven — PL Semantics and Symbolization
It is recommended that you
print this reference.
Contents: Section
1: Semantics; Section 2: Basic
Forms; Section 3: Categorical Logic; Section
4: Complicated Symbolization
This chapter provides the semantics for PL along with details on how this artificial language relates to English.
1. Semantics
Interpretations | Truth Conditions | Basic Concepts for PL
We now give the semantics for PL; that is, we will say what it means for a PL sentence to be true and then revist our basic semantical concepts (like validity, logical equivlence, and so forth). As with SL, we define the semantics by providing truth conditions. Truth conditions presuppose the notion of an interpretation. So, we start there.
Interpretations
A PL sentence is true or false only given an interpretation. So, first we need to specify just what an interpretation is.
Before giving an exact definition, we should say that an interpretation is basically the association given by a symbolization key. For example, we have for symbolization purposes considered the following sort of association:
| The universe of discourse: | Women in the US Senate. |
| Cx: | x is from California |
| Sxy: | x is senior to y (in the Senate) |
| b: | Barbara Boxer |
| f: | Diane Feinstein |
This symbolization key specifies an interpretation for a small part of PL: the two predicate letters 'C' and 'S' and the two names 'b' and 'f'. In general, an interpretation needs to specify an association for all names and predicate letters of PL. And the interpretation needs to be spelled out a bit more exactly than (for instance) just associating 'Sxy' with the vague English "x is senior to y". Even "is from California" is a bit vague. (Born in? Elected by?) Instead, an interpretation associates 'S' with a precise group or relation of objects in the the universe of discourse.
But other than these scruples, an interpretation is just that described by a symbolization key. Bear that in mind as you read...
An interpretation for PL is an assignment of meaning which specifies a) a universe of discourse, b) the members of the universe of discourse to which any one-place predicates apply, c) the relationships between members of the universe of discourse to which any 2 or more-place predicates apply, d) the truth value of any 0-place predicate letters and e) the objects named by any individual constants.
Thus, our symbolization key above describes an interpretation but only to a small part of PL and only in a rather vague way. Often though, the vague and partial association is a good enough specification of an interpretation.
Truth Conditions
For atomic sentences of PL (like 'Cb' or 'Sbf') the truth is to be "read off" the interpretation. Yes, Boxer's contained in the group from California (as the interpretation specifies) so Cb is true.
As with SL, we can specify truth conditions for a complex sentence in terms of its parts. When the main connective of the PL sentence is a truth functional connective, '&', 'v', '>', '=', or '~', the truth conditions are given just as before. So, for example, a sentence P of SL that is a conditional, P = Q>R, is true on an interpretation I just in case either Q is false on interpretation I or R is true on I. (That is, the only way for Q>R to be false is for P to be true on I and R false: just like SL.)
There is one main complication for the semantics of PL: the quantifiers. Specifically, when a quantifier is the main connective of a sentence (for examples (^x)P or (%y)Q ) we cannot understand the truth value of the complex sentence in terms of the truth value of its part. Why not? Because P and Q are usually formulas but not sentences so are neither true nor false!
Instead, we need to describe the substitution instances of a quantified sentence in order to define its truth conditions. (Bear in mind from the tutorial that this definition is a little tricky! You may want to review that material.)
In general, the quantifier's semantics stated in terms of substitution instances needs to be defined in the presence of names for all members of the universe of discourse. So, if we need to evaluate the truth value of a sentence of PL with respect to an interpretation lacking names for some elements of its universe of discourse, we simply add names to the interpretation until each member has a name and then evaluate.
'(^x)P' is true on an interpretation I if and only if P(a/x) is true on I for all names a (where names for all members of the universe of discourse are added if necessary).
Similarly,
'(%x)P' is true on an interpretation I if and only if P(a/x) is true on I for at least one name a (where names for all members of the universe of discourse are added if necessary).
(Of course, when adding names, we leave the rest of the given interpretation unchanged.)
Basic Concepts for PL
Now we can give the rest of the semantical definitions.
For example, to give the definition of logical truth in PL we take the old SL definition:
A sentence of SL in logically true in SL if and only if it is false on no truth value assignment.
and replace the words "truth value assignment" with "interpretation":
A sentence of PL in logically true in PL if and only if it is false on no interpretation.
After all, a truth value assignment is just an interpretation for SL (where there are no names, predicates, or relations to interpret.) The basic idea of a logical truth remains that there is no way for it to be false, i.e., no interpretation making it false.
The rest of the definitions are just as easy to convert. Here are the results.
A sentence of PL is logically false in PL if and only if it is true on no interpretation.
A sentence of PL is logically indeterminate in PL if and only if it is true on no interpretation.
An argument is valid in PL just
in case there is no interpretation on which its conclusion is
false and its premises are all true.
An argument is invalid
in PL if and only if it is not valid in PL, i.e., if and only if
there is a interpretation making its premises true and conclusion
false.
Similarly,
The two members of a pair of PL sentences are logically equivalent in PL if and only if there is no interpretation making on which one of the pair is true while the other is false.
And...
A set of PL sentences is logically consistent
in PL if and only if there is some interpretation on which
all members of the set are true.
A set of PL sentences is logically inconsistent
in PL if and only it it is not logically consistent, i.e., there
is no interpretation on which all members of the set are true.
2. Basic Forms for PL Symbolization
It may be best to see languages (like English) as having two basic quantificational forms: the existential and the universal.
Existential Form
The first basic form of English is the following.
existential form: Some S are P.
where 'S' (the subject) and 'P' (the predicate of the expression) name groups or classes of individuals. (We will call these the subject class and the predicate class, respectively.)
So, for example. "Some students are freshman" is of existential form. And it's pretty easy to see how it might be symbolized. Given a natural symbolization key, it could well be rendered as '(%x)(Sx&Fx)'. For such an easy example, we don't need to think of forms. But for more complicated cases it's best to fit the "mold".
Take this example,
(*) There are female logic students who are juniors set to graduate next year.
Ugh! But we can fit this messy example sentence into the existential form and then symbolize. The following steps will help as you consider such a sentence.
First, here's the mold we need to fit:
(Step I) Some S are P.
Begin by noting that (*) is about "female logic students". So, this is the subject class. And the predicate class, which (*) attributes to its subject is "juniors who will graduate next year".
Now, we need to provide a hybrid English, PL symbolization of the form:
(Step II) (%x)(x is an S & x is a P)
For (*) this should be "(%x)(x is a female logic student & x is a junior set to graduate next year)".
Finally, we take the hybrid of step II and form it into pure PL:
(Step III) (%x)(Sx & Px)
For (*) this means rewriting the subject phrase "x is a female logic student" and the predicate phrase "x is a junior set to graduate next year" into PL. Take this key:
| universe of discourse: | People |
| Fx: | x is female |
| Jx: | x is a junior |
| Sxy: | x is a student of subject y |
| Gxy: | x will graduate in year y |
| l: | logic |
| n: | next year |
Then the subject phrase becomes: 'Fx&Sxl' and the predicate phrase becomes 'Jx&Gxn'. So, finally we have:
(*)'s Symbolization: (%x)[ (Fx&Sxl) & (Jx&Gxn) ]
Many different English sentences can likewise be seen to fit this form. You may want to review the tutorial for details. In all cases, you move from seeing the English as about a subject and predicate class to a PL symbolization of form (%x)(Sx & Px).
Universal Form
The second form is for sentences saying that all such-and-such are so-and-so. For example, "All Swedes are Europeans". Again we have a subject class and predicate class:
universal form: All S are P.
Such a universal statement means that anything is such that if it's in the subject class, then it's also in the predicate class. So, our example might be translated as '(^x)(Sx>Ex)'.
In general, we have the same three step process as for existential form. First we need to see that the English sentence is of a form relating a subject to a predicate in the appropriate way:
(Step I) All S are P
Next, we move to the hybrid form:
(Step II) (^x)( x is an S > x is a P )
Finally we give the symbolization.
(Step III) (^x)(Sx>Px)
For another example of universal form, think about
(**) Every female juniors will graduate next year.
This means:
(Step I) All female juniors are people who will graduate next year.
Notice that the subject is a conjunction. So, we have the hybrid form:
(Step II) (^x)( x is a female and a junior > x is a person who will graduate next year )
and finally the symbolization:
(Step III) (^x)( (Fx&Jx) > Gxn )
Almost all sentences you'll be asked to translate are of these two basic forms or are made out of sentences of these two forms. But many are fairly complicated. Think about translating "All logic students who will graduate next year are female and now juniors"!
3. Categorical Logic
Categorical logic treats relationships between the types of things (categories) which satisfy one-place predicates. We can use PL to quickly get at the heart of this logic because categorical forms are built from existential and universal form sentences.
Categorical logic recognizes four main types of statement:
| Type | English Form | PL Form |
|---|---|---|
| A-form: | All S are P | (^x)(Sx>Px) |
| E-form: | No S are P | (^x)(Sx>~Px) or ~(%x)(Sx&Px) |
| I-form: |
Some S are P |
(%x)(Sx&Px) |
| O-form: | Some S are not-P | (%x)(Sx&~Px) |
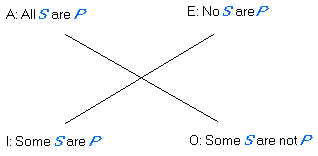
Notice from this table that A-form and I-form are (respectively) just what we call "universal" and "existential" forms. The E-form is either universal with negated consequent or negated existential. And the O-form is existential with negated second conjunct.
Now notice that A and O form sentences are "opposites": if one is true, then the other is false. The same relation of opposition holds between E and I forms. We call such pairs contradictories. This fact is represented in the following table:
|
(Pairs of sentences connected by diagonal lines are contradictory.) |
Developed in ancient Greek times, categorical logic was the first systematic logic. "Aristotle" is the main name in this development. He also was the first systematizer of many of the sciences; quite an accomplishment!
However, Aristotle's categorical logic differed a bit from the treatment just described. Most important, he and his contemporaries thought that there were further significant logical relationships besides the oppositions shown in the modern square pictured above. For instance, it was thought at the time that sentences of A and E form but with identical subject and predicates could not both be true and that a similar pair of I and O form sentences could not both be false.
But PL and modern logic do not agree with the ancient thinking. To see the dispute in focus, one needs only to consider a few examples. First, take this pair on which we'll all agree:
All whales are mammals.
No whales are mammals.
These two sentences are not both true. Of course, only the first is.
Now, for the disagreement between ancient and modern logic, consider this pair:
All Martians are green.
No Martians are green.
On the ancient treatment, both these sentences are false. But note that when we translate them into PL we get:
(^x)(Mx>Gx)
(^x)(Mx>~Gx)
Because the subject term of both is empty, there are no Martians!, it follows from the definition of '>' and '^' that both are true!
What seems most strange about this is that we are saying that "All Martians are green" is true if we side with modern logic and the PL symbolization of universal form sentences. Thus we see one reason for the ancients to object to modern logic.
However, it's worth seeing the motivating idea for the modern claim that "All Martians are green" should count as true. To get this idea, suppose for a moment that the Aristotelians are right after all, and that "All Martians are green" is false. This would mean that "Not all Martians are green" is true. Now, doesn't the truth of such a statement make you ask: "Well, if not all Martians are green, then what color are those which aren't green?" That is, it seems intuitive to respond to the ancient view: "well, if not all Martians are green, then some must be red or blue or some other color"!
What the modern logician does here is a version of our indirect proof (the basis for the derivation rules ~E and ~I). She takes the Aristotelian position:
"All Martians are green" is false
And shows this amounts to the claim that
"Not all Martians are green" is true
so that the Aristotelian is committed to the idea that
"There are Martians who are of a color different from green" is true.
This is an unfortunate consequence, to say the least. We should say that the Aristotelian position has been "reduced to absurdity". (One's logic alone shouldn't prove that there are funny colored Martians!) Thus, the modern logician does not accept the Aristotelian understanding of A-form (universal form) sentences.
4. Complicated Symbolization
There are number of complications for symbolizing English sentences in PL. In Tutorial 7.2, we noticed that many English sentences are of either Existential ("Some S are P") or Universal ("All S are P") form. Often, though, this means a complicated subject, S, or predicate, P. Tutorial 7.3 takes up three sorts of complication:
- Wording may make the call between existential and universal form unclear or ambiguous.
- There may be more than one quantifier to symbolize, one within the scope of the another.
- A complex subject or predicate of a categorical statement may itself have an Existential or Universal form!
- Some words in English provide a restricted quantification.
So keep these complications in mind as you symbolize.
As a reminder, the main examples from Tutorial 7.3 are repeated below.
Wording Complications
1) Every male student is a friend of Jenny.
The "every" indicates a universal quantification. It's pretty easy to see how to fit this into the universal form mold:
(^x)( x is a male student > x is a friend of Jenny )
Then, symbolize using: 'Mx' for "x is a male", 'Sx' for "x is a student", 'Fxy' for "x is a friend of y", 'j' for "Jenny".
(^x)( (Mx&Sx) > Fxj )
2) Each of Tom's male friends is a friend of Jenny.
Here too we need to fit the universal quantification mold:
(^x)( x is a male friend of Tom > x is a friend of Jenny )
To say "x is a male friend of Tom's" is to say that x is male and a friend of Tom's: '(Mx&Fxt)'. So, 2)'s symbolization is
(^x)( (Mx&Fxt) > Fxj )
3) A male friend of Tom is a friend of Jenny.
This is like 2) but is of existential form. So, to fit the mold, we have:
(%x)( x is a male friend of Toms & x is a friend of Jenny )
Which is symbolized as
(%x)( (Mx&Fxt) & Fxj )
Next, let 'i' be a name for the author of these lines and consider
4) A friend of Tom is a friend of mine.
Notice that this could easily be taken as either of universal or existential form. It might mean any friend of Tom is my friend too, or just that some person is friend of both of us. So, 4) is ambiguous and can be symbolized as either
(^x)( Fxt > Fxi )
or
(%x)( Fxt & Fxi )
The word "any" is likewise a bit confusing.
5) If anyone joins me, I'll be happy for the help.
Which means that if even one person joins me I'll be happy. But this "even one person" is a simple existential quantification:
(%z)Jzi > Hi
Here, as before, 'i' stands for me. 'J' stands for the joining relation, and 'H' for the "is happy" predicate. So, 5) is not of existential form. Instead, it's a conditional.
Contrast this with the apparently similar:
6) If anyone joins me, he or she will be happy.
This statement does not say of one person that he or she will be happy, instead: "All people are such that if they join me, they'll be happy". So the symbolization of 6) is as follows:
(^x)(Jxm > Hx)
Notice that we have to have the larger scope here. Without the parentheses around 'Jxm > Hx', this would not even be a sentence.
Very typically, when the larger scope is required -- when the quantified variable appears in both antecedent and consequent, we will have universal form.
Another example:
7) If someone joins me, he or she will be happy.
Oddly, this means the same as 6 and is of universal form! The "someone" is any person. So this is symbolized as with 6:
(^x)(Jxm > Hx)
8) All ravens and starlings are birds.
Utilizing the obvious symbolization key, try to think about why the following is incorrect:
WRONG!: (^x)[ (Rx&Sx) > Bx ]
Clearly, 8) does not have as its subject "things which are both ravens and starlings. There are no such things. So, it's a mistake to see 8) as of universal form. Instead, it means that all ravens are birds and all starlings are birds. So, 8) is:
(^x)(Rx > Bx) & (^y)(Sy > By)
So, 8) expresses the same thing as a pair of universal form sentences. But 8) could also be symbolized as
(^x)(( Rx v Sx ) > Bx)
So, the subject can be seen as things in either the group of ravens or starlings.
Suppose the universe of discourse is counting numbers, (1,2,3,4, etc.) and 'Gxy' stands for "x is greater than y".
9) For every number there exists a greater one.
I.e.,
For every number x there exists a y which is greater
or
(^x)(%y)Gyx
But notice that it would be very different to say
10) There exists a number greater than all numbers.
This last, 10), is false! There is no greatest counting number; they get larger and larger.
Still we can symbolize 10):
(%y)(^x)Gyx
Compare this to the symbolization of the true 9). Quantifier order makes all the difference here.
Complex Subjects and Predicates
Moving back to a universe of discourse of OU students, consider
11) Everyone who has a friend is a friend of Jenny.
This is best fit slowly into the universal form.
(^x)( x has a friend > x is a friend of Jenny )
The only difficulty here is the subject clause; it too involves a quantifier. The indefinite article "a" becomes '%' in the symbolization:
(^x)( (%y)Fyx > Fxj )
12) Everyone who has a friend is the friend of every male.
Which goes to the hybrid form:
(^x)( x has a friend > x is the friend of every male )
So, now both subject and predicate involve additional quantifiers. The subject is just like 11). The predicate is another universal form expression: every male has x as friend. So, we get:
(^x)( (%y)Fyx > (^z)( Mz > Fxz ) )
Restricted Quantification
One complication we've ignored until now is the difference between "everyone" or "everybody" and "everything". We've been able to conflate these quantifiers of English when our universe of discourse included only people. 12) just above is an example: we were concerned only with people at OU.
But change our universe of discourse to living creatures at the zoo. It's quite different to say "everyone is happy" (maybe true!) rather than "everything is happy". To symbolize "everyone is happy", we need to see that this means "for every x, if x is a person, then x is happy".
In general (where we can't suppose a universe of discourse to include only people), we should symbolize as follows:
|
Hybrid Form
|
Symbolization
(Px: x is a person; Qx: x is Q) |
|
Everybody is Q.
or Everyone is Q. |
(^x)(Px>Qx)
|
|
Somebody is Q.
or Someone is Q. |
(%x)(Px&Qx)
|
So, while universe of discourse is everything at the zoo, 'Hx' stands for "x is happy", and 'Px' stands for "x is happy",
13) Someone at the zoo is happy.
could be symbolized as
(%x)(Px&Hx)
A last thought. Symbolization is tricky because natural language is so complicated. But that's exactly why symbolizing is worthwhile: we get a better understanding of language. And just a few days hard work goes a long way in this study: lots of practice at the problem sets will give you a sophisticated grasp of subtleties in English!
back to chapter seven
on to the next chapter
continue with this reference