A Turing Machine is a very basic computing device that follows directions for manipulating simple symbols on a "tape". The symbols, for example, may be just zeros and ones. The machine starts in initial state, we'll still call this state "1" and reads the first symbol written on the tape.
Here's that picture again. The tape describes a subtraction problem...
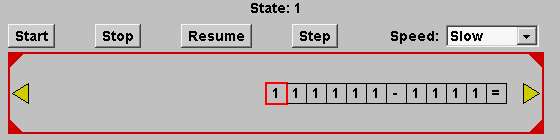
Notice that the numbers involved are represented non-standardly. The subtraction problem represented is 6 - 4. How come? This is a unary representation of the numbers.
Now, to program this thing, we need to give it directions.
For example, the first direction to the machine may be
Direction One: If you are in state 1 and the input you read is "1", then stay in state 1, leave the "1" and move RIGHT.
What good is this direction? Not much in itself; it only begins scanning the numerals. But we'll see that we can put lots of these directions together to make a program which calculates.
Before we do this, we'll need a more compact way to rewrite Direction One:
Compact Form: 1,1 1,1,>
This just means the same thing, but it's easier to write.
On the link below you'll be taken to a page that provides a working Turing Machine. But you'll need to program it!
- First load and run the Subtraction program to see how it works.
- Then try to do something on your own. Maybe get the machine to add!
- And you might think about using binary representations.
- Finally think about how you might code up other problems...you'll use symbols to represent something besides numbers. Perhaps you would use numerals to represent the programs, English, etc.
Here's the Turing Machine (from the web pages of Suzanne Skinner)
Return Home